Question

A 15.0 kg box is being pulled along level ground at a constant velocity by a horizontal force of 38.0N.What is the coefficient of the kinetic friction between the box and the floor?

Answer 1

Newton's second law states that:

`\vec{F}=m\vec{a}`

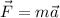
where F denotes the net force acting on the object. In this case we know that the box is moving at constant velocity that means that the acceleration has to be zero; then the net force has to be also zero, that is:

`\vec{F}=\vec{0}`

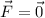
Now, since we have forces acting in two directions the vector equation above can be written as two equations, one for the x component and one for the y component.

The x components equation is:

`38-f_k=0`

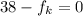
The y components equation is:

`N-W=0`

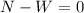
Now, from the first equation we have that the force of friction is:

`f_k=38`

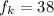
but we have to remember that the force of frcition is related to the normal force as:

`f_k=\mu_kN`

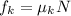
Then we have:

`\mu_kN=38`

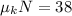
Now, from the second equation of motion given above (the y component) we have that:

`N=W`

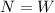
plugging this in the previous equation we have that:

`\begin{gathered} \mu_kN=38 \\ \mu_kW=38 \\ \mu_k=(38)/(W) \\ \mu_k=(38)/((9.8)(15)) \\ \mu_k=0.259 \end{gathered}`

Therefore the coefficient of friction is 0.259 (rounded to three decimal places).