Question

Write an equation describing the relationship of the given variables. If you need to type an exponent use the "^" key (shift+6) to indicate the power. For example, x squared (x times x) can be typed as x^2. One variable will go within each submission box. If multiple variables are on one side of the equation then type them in alphabetical order.y varies jointly as the square of x, the square of z, and when x=3 and z=4, then y=72The equation is:Answer = AnswerAnswerAnswer

Answer 1

`y\text{ = }(1)/(2)x^2z^2`

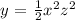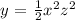
Step-by-step explanation:

Given:

y varies jointly as the square of x and square of z

Mathematically:

`\begin{gathered} y\text{ }\propto x^2z^2 \\ To\text{ equate the expression:} \\ y\text{ = k}x^2z^2 \\ \text{where k = constant of proportionality} \end{gathered}`

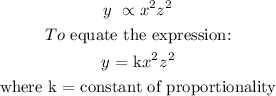
when x = 3 and z = 4, y = 72

We need to find the value of the constant of proportionality, k

Substitute for x, y and z in the equation above:

`\begin{gathered} 72=k(3^2)(4^2) \\ 72\text{ = k(9)(16)} \\ 72\text{ = }144k \\ \\ \text{divide both sides by 144:} \\ (72)/(144)\text{ = }(144k)/(144) \\ k\text{ = 1/2} \end{gathered}`

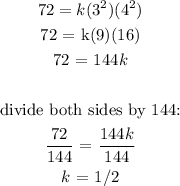
The equation showing the relationship between x, y, and z:

`y\text{ = }(1)/(2)x^2z^2`