Solving for the volume of the cube.
Recall the formula for solving the volume of the cube.

Given a side length of 7 units, substitute s = 7, and we have
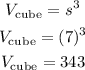
Therefore, the volume of the cube is equal to 343 cubic units.
Solving for the side length of the square.
Recall the area of the square
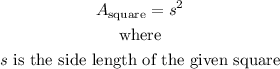
Given that the area of the square is equal to 13 square inches, substitute A = 13 and we get
![\begin{gathered} A_{\text{square}}=s^2 \\ 13=s^2 \\ \\ \text{Take the square root of both sides} \\ \sqrt[]{13}=\sqrt[]{s^2}^{} \\ s=\sqrt[]{13} \\ s\approx3.6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8uh918olxnu0d6etm0zvffylhde5e44uzt.png)
Therefore, the side length of the square is the square root of 13 units or approximately 3.6 units