Question

The first four terms of a sequence are shown.1/8, 1, 8, 64, ...Which expression can be used to find the nth term in the sequence?A. 1/8(8)^n-1B. 8(1/8)^n-1C. 1/8(8)^nD. 8(1/8)^n

Answer 1

First we need to find the common ratio of the sequence. We do this by dividing each number by the previous number to it:

`(1)/((1)/(8))=8`
`(8)/(1)=8`
`(64)/(8)=8`

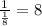
So the common ratio "r" is 8:

`r=8`

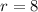
Now we can use the formula to find the nth term of a sequence:

`a_n=a_1r^(n-1)`

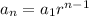
Where "an" is the nth term, "a1" is the first term which in this sequence is 1/8, and "r" is the common ratio which is 8. Substituting this we get the expression that can be used to find the nth term in the sequencehe sequenc:

`a_n=((1)/(8))(8)^(n-1)`

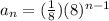
Thus, the answer is option A: 1/8(8)^n-1