Question

The admission fee at an amusement park is $4.25 for children and $7.00 for adults. On a certain day, 316 people entered the park, and the admission fees collected 1893 dollars. How many children and how many adults were admitted?numbers of children equals ____number of adults equals ____

Answer 1

We want to calculate the exact number of children and the exact number of adults that attended this particular day.

Let x be the amount of children and y the amount of adults.

We are told that a total of 316 people entered the park this day. So, the total amount of people is simply the sum of children and adults. That leads to the equation

`x+y=316`

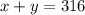
Now, if we multiply 4.25 times x, we would get the total collected amount for the admission fees of the children. If we do the same with the adults (7*y) we would get the total amount collected for the admission fees of the adults. This two quantitiies would represent the total amount of collected money for admission fees. Then, we have the equation

`4.25x+7y=1893`

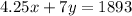
From the first equation we can find that

`x=316\text{ -y}`

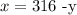
Now, we can replace this in the second equation, so we get

`4.25\cdot(316\text{ -y) + 7y=1893}`

If we distribute on the left side, we get

`4.25\cdot316\text{ - 4.25y + 7y = 1343 + 2.75y=1893}`

now, we can subtract 1343 from both sides, so we get

`2.75y=1893\text{ - 1343=550}`

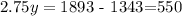
Finally, we divide both sides by 2.75, so we get

`y=(550)/(2.75)=200`

Now, we replace this value in the expression we found for x, so we get

`x=316\text{ -y = 316 - 200 = 116}`

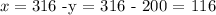
So there were 116 children and 200 adults.