Answer: D. Graph D assuming that it is the last one shown.
Step-by-step explanation
Given

we can determine the solutions of the equation (the points at which y = 0) and compare them with the graphs given to see which one is the correct one.
To solve the equation, we have to set it to 0:
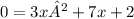
Now, we can use the General Quadratic Formula to solve it:
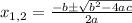
where a, b and c represent the coefficients of the equation in the form:

Thus, in our case a = 3, b = 7, and c = 2. Replacing the values in the General Quadratic Formula and solving:
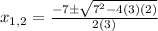

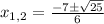

Finally, calculating our two solutions:
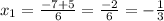
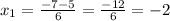
Based on these values, we can see that the graph that has two solutions in the negative numbers is: