1 Answer

James Schek · Answer 1 · 2023-10-09T17:10:51+0000

Given the inequality:

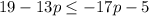
$19-13p\leq-17p-5$

You can find the solution as follows:

1. Apply the Subtraction Property of Inequality by subtracting 19 from both sides of the inequality:

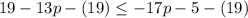
$19-13p-(19)\leq-17p-5-(19)$
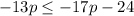
$-13p\leq-17p-24$

2. Apply the Addition Property of Inequality by adding this term to both sides of the inequality:

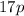
Then:

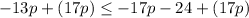
$-13p+(17p)\leq-17p-24+(17p)$
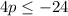
$4p\leq-24$

3. Apply the Division Property of Inequality by dividing both sides of the inequality by 4:

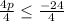
$(4p)/(4)\leq(-24)/(4)$
$p\leq-6$

Hence, the answer is:

$p\leq-6$

Please log in or register to add a comment.