Given data:
* The value of forces acting on the block is,
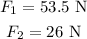
* The mass of the block is m = 8 kg.
* The angle of the force F_2 with the horizontal is,
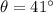
Solution:
The horizontal component of the force F_2 is,
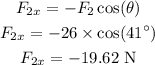
Here, the negative sign indicates the direction of the horizontal force is towards the negative of the x-axis.
The vertical component of the force F_2 is,
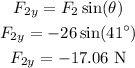
There is no motion of the block takes place in the vertical direction, thus, the normal force acting on the block is,

Thus, the net force acting in the vertical direction is,

According to Newton's second law, the acceleration of the block in the vertical direction is,

The net force acting on the block in the horizontal direction is,
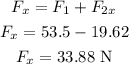
According to newton's second law, the acceleration of the block along the horizontal direction is,
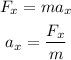
Substituting the known values,
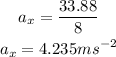
The magnitude of the acceleration is,
![\begin{gathered} a=\sqrt[]{a^2_x+a^2_y} \\ a=\sqrt[]{(4.235)^2+0} \\ a=4.235ms^(-2) \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/npdnmhkicmodru4t2qbiic6igf9qslxtu3.png)
The direction of the acceleration is,
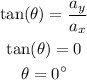
Thus, the magnitude of the acceleration is 4.325 meters per second squared and the direction of the acceleration is towards the right (positive x-axis).