Question

Multiply the rational expressions and express the product in simplest form. When typing your answer for the numerator and denominator be sure to type the term with the variable first.The numerator is AnswerThe denominator is Answer

Answer 1

• The numerator is x+5.

,

• The denominator is x+3.

Step-by-step explanation:

Given the expression:

`(\left(x^2-x-6\right))/(\left(2x^2+x-6\right))\cdot(\left(2x^2+7x-15\right))/(\left(x^2-9\right))`

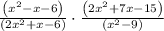
First, factor each of the quadratic expressions where possible.

`\begin{gathered} ((x^2-3x+2x-6))/((2x^2+4x-3x-6))\cdot((2x^2+10x-3x-15))/((x^2-3^2)) \\ =(x(x-3)+2(x-3))/(2x(x+2)-3(x+2))\cdot\frac{2x(x+5)-3(x+5)}{(x-3)(x+3^{})} \\ =((x-3)(x+2))/((2x-3)(x+2))\cdot\frac{(2x-3)(x+5)}{(x-3)(x+3^{})} \end{gathered}`

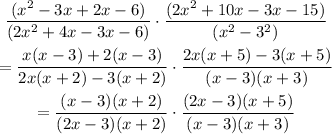
Next, cancel the common factors in the numerator and denominator:

`\begin{gathered} ((x-3)\mleft(2x-3\mright)(x+2))/((x-3)(2x-3)(x+2))\cdot\frac{(x+5)}{(x+3^{})} \\ =(x+5)/(x+3) \end{gathered}`

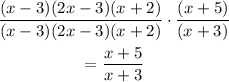
• The numerator is x+5.

,

• The denominator is x+3.