Question

Solve by graphing 3x^2 + 5x - 2 = 15. Find the x-values and type their numerical values in the two blanks provided. Round each result to the nearest thousandth.

Answer 1

To graph the quadratic function you have to determine the coordinates of its vertex and the roots (x-intercepts)

1) To find the roots of the function, the first step is to zero it:

`\begin{gathered} 3x^2+5x-2-15=15-15 \\ 3x^2+5x-17=0 \end{gathered}`

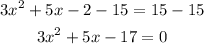
Next, you have to identify the coefficients of the function:

"a" represents the coefficient of the squared term, for this function a= 3

"b" is the coefficient of the x-term, for this function b= 5

"c" is the constant of this function, in this case, c= -17

Use the quadratic function to calculate the possible x-intercepts:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Replace the formula with the coefficients:

`\begin{gathered} x=\frac{-5\pm\sqrt[]{5^2-4\cdot3\cdot(-17)}}{2\cdot3} \\ x=\frac{-5\pm\sqrt[]{25+204}}{6} \\ x=\frac{-5\pm\sqrt[]{229}}{6} \end{gathered}`

Solve the addition and subtraction separately:

Addition:

`\begin{gathered} x=\frac{-5+\sqrt[]{229}}{6} \\ x=1.689 \end{gathered}`

Subtraction:

`\begin{gathered} x=\frac{-5-\sqrt[]{229}}{6} \\ x=-3.355 \end{gathered}`

The roots of the function are x=1.689 and x=-3.355

2) To determine the coordinates of the vertex, you have to use the following formula to determine the x-coordinate (h):

`h=(-b)/(2a)`

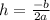
Replace it with b=5 and a=3

`h=-(5)/(2\cdot3)=-(5)/(6)`

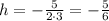
Next, replace the value of x into the function to calculate the corresponding y-coordinate (k)

`\begin{gathered} k=3x^2+5x-17 \\ k=3(-(5)/(6))^2+5\cdot(-(5)/(6))-17 \\ k=3\cdot(25)/(36)-(25)/(6)-17 \\ k=(25)/(12)-(25)/(6)-17 \\ k=-(229)/(12)\approx-19.083 \end{gathered}`

The coordinates of the vertex are (-0.833,-19.083)

Plot the points and graph the quadratic function:

Note that the coefficient of the quadratic term is positive, this indicates that the parabola opens upwards.