Question

Hello I seem to be having some difficulty with this question can you please help me thank you

Answer 1

a. 6188 ways

b. 752560 ways

We need to find how many ways we can choose 5 colors from 17 distinct colors.

From this we know that:

n = total number of colors in the set = 17

r = number of choosing colors = 5

If the choices are not relevant, we will use Combination which is noted as:

`nCr=(n!)/(r!(n-r)!)`

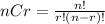
Substitute the values of n and r:

`\begin{gathered} nCr=(17!)/(5!(17-5)!) \\ =6188 \end{gathered}`

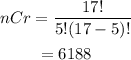
When the order of choices is not relevant, there are 6188 ways to choose 5 colors out of 17.

Now, if the order of choices is relevant, we will use permutation which is noted as:

`nPr=(n!)/((n-r)!)`

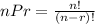
Again, substitute the values of r and n:

`\begin{gathered} nPr=(n!)/((n-r)!) \\ nPr=(17!)/((17-5)!) \\ =742560 \end{gathered}`

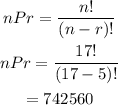
When the order is relevant, there could be a total of 752560 ways of choosing 5 colors