The Determinant of this matrix must be different from 0 so that its inverse can be found
So we calculate The determinant
this is the matrix on a general form
We apply a equation to find Determinant
The equation
And we replace for our case
then
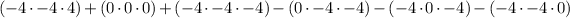
and solve, first parethesis
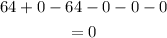
this determinant is zero so the matrix has no inverse matrix
The inverse of the matrix A is no possible