Step 1. The information that we have is:
• 200 tickets are sold at a price of $5
,
• 10 will win a prize of $20
,
• 4 will win a prize of $15
,
• 1 will win a prize of $50
Required: Find the expected value of buying a ticket.
Step 2. We will find the value of the ticket for each case and its probability.
For those 10 people who bought a $5 ticket and won a $20 prize, the value of their ticket was:
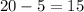
And the probability of being one of those 10 people for whom the ticket is worth $15 is:
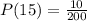
Step 3. For the 4 people who will win a $15 prize, the value of their ticket was:
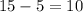
We subtract 5 because of the initial ticket they bought.
And the probability of being one of those people for whom the ticket is worth $10 is:
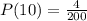
Step 4. One will win a prize of $50, for that person, the value of their ticket is:
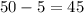
And the probability of being the person for whom the ticket is worth $45 is:
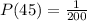
Step 5. For the rest of the people (the rest is 185 people) who do not win any prize, the value of their ticket is a negative 5 because they spent $5 on the ticket but do not win any prize.
The probability of being one of those people for whom the ticket value is -$5 is:
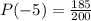
Step 6. To summarize, we can make a table where x is the value of the ticket and P(x) is the probability:
Step 7. The expected value is found using the formula:

Where each term represents the multiplication of one x value and its probability.
The result is:
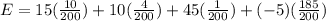
Making the operations:
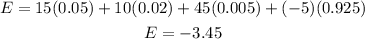
The expected value is -$3.45
Answer:
-3.45