Part a
For this case we have two points given (1,3) and (4,6) and we want to find the equation for this line and we can use this equation:

Where m represent the slope and b the intercept. We can estimate the slope with this formula:

And then we can find the intercept from one point given and replacing into the equation like this:
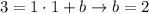
And the equation would be:
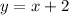
Part b
Now we just need to see if the point (1,3) is on the line calculated let's check this. If x=1 we have that:

So then we verify that the point is on the line and then that would be the proof for this case.