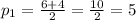Question

If the equation x2 −3x+1= p(x−3) has equal roots, find the possible value(s) of p.

Answer 1

Answer: p = 5, p = 1

Step-by-step explanation

Given

`x^2−3x+1=p\left(x−3\right)`

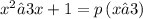
Since the roots are equal, then the discriminant must be 0:

`b^2-4ac=0`

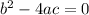
where a, b and c are the coefficients of the quadratic expression in the form ax² + bx + c = 0. Then, we must rearrange our equation in the previous form.

0. Multiplying ,p, times the expression inside the parenthesis:

`x^2−3x+1=p\cdot x−3p`

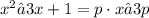
2. Setting the expression to 0:

`x^2−3x-px+1+3p=0`

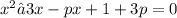
2. Simplifying the expression by grouping similar terms:

`x^2-(3+p)x+(1+3p)=0`

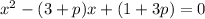
Then, in our case: a = 1, b = –(3 + p), and c = (1 + 3p).

Now, we can replace the value in the discriminant and solve for p:

`(-(3+p))^2-4(1)(1+3p)=0`
`(-3-p)^2-4(1+3p)=0`
`(-3-p)^2-4+12p=0`
`p^2-6p+5=0`

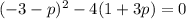
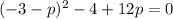
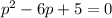
Finally, we can use the General Quadratic Expression to solve for p:

`p_(1,2)=(-(-6)\pm√((-6)^2-4(1)(5)))/(2(1))`
`p_(1,2)=(6\pm√(36-20))/(2)`
`p_(1,2)=(6\pm√(16))/(2)`
`p_(1,2)=(6\pm4)/(2)`

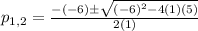
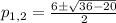
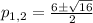
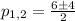
Now, calculating both results:

`p_1=(6+4)/(2)=(10)/(2)=5`
`p_1=(6-4)/(2)=(2)/(2)=1`