Given the triangles RST and DEF, you know that:
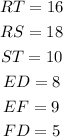
(a) Knowing the corresponding sides, you get these ratios:
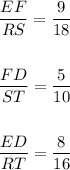
Notice that you can simplify the first ratio by dividing the numerator and the denominator by 9:
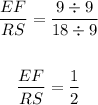
Simplify the second ratio dividing the numerator and the denominator by 5:

Simplify the third ratio dividing the numerator and the denominator by 8:
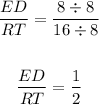
(b) By definition, two angles are congruent when their measures are equal.
In this case, you know that the corresponding sides of the triangles are in proportion. Then, you can conclude that their corresponding angles are congruent:
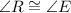
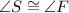

(c) By definition, two triangles are similar when the lengths of their corresponding sides are in equal proportion and their corresponding angles are congruent.
In this case, knowing that the lengths of the corresponding sides of both triangles are in equal proportion and also knowing that their corresponding angles are equal, you can conclude that the triangles are similar.
Hence, the answers are:
(a)
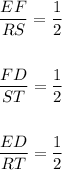
(b)
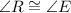
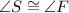

(c) First option.