Question

Find the volume of the composite solid. Round your answer to the nearest tenth.

Answer 1

`\bold{\huge{\green{\underline{ Solution }}}}`

Given :-

• The height of the cylinder is 26 cm
• The base of the cylinder is 12cm
• The base diameter of hemisphere is 12cm

To Find :-

• We have to find the volume of composite solid.

Let's Begin :-

For cylinder,

• Height = 26 cm
• Base diameter = 12cm

Therefore,

The radius of the cylinder will be

`\sf{=} {\sf{( Diameter)/(2)}}`

`\sf{=}{\sf{( 12)/(2)}}`

`\sf{ = 6 cm}`

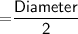
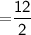
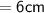
Thus, The radius of cylinder is 6 cm

Now, we know that,

Volume of cylinder = πr²h

Subsitute the required values,

`\sf{ = 3.14 × 6 × 6 × 26}`

`\sf{ = 2939.04 cm³}`

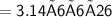
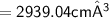
Now, For Hemisphere

• Base diameter = 12cm

Therefore,

The radius of the hemisphere will be

`\sf{=} {\sf{( Diameter)/(2)}}`

`\sf{=}{\sf{( 12)/(2)}}`

`\sf{ = 6 cm}`

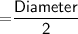
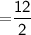
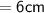
We know that,

Volume of hemisphere = 2/3πr³

Subsitute the required values,

`\sf{ = 2/3× 3.14 × 6 × 6 × 6}`

`{\sf{=}}{\sf{( 1356.48)/(3)}}`

`\sf{ = 452.16 cm³}`

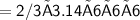
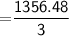
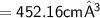
Thus, The volume of hemisphere is 452.16 cm³

Therefore ,

Area of composite solid

`\sf{ = 2939.04 + 452.16}`

`\sf{ = 3391.2 cm³}`

`\sf{ = 3391 cm³}`

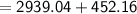
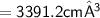
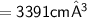
Hence, The total volume of composite solid is 3391 cm³