2 Answers

Sammiepls · Answer 1 · 2023-08-01T01:42:46+0000

The area of an oblique pyramid is one-third of the product of the area of the base and its height.

Thus, we substitute the values of the dimensions to the following equation.

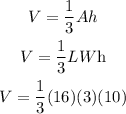
$\begin{gathered} V=(1)/(3)Ah \\ V=(1)/(3)LW\text{h} \\ V=(1)/(3)(16)(3)(10) \end{gathered}$

Simplify the expression by cancelling out the 3 from the numerator and the denominator. Thus, we get the following.

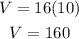
$\begin{gathered} V=16(10) \\ V=160 \end{gathered}$

Therefore, the volume of the pyramid is 160 in³.

Please log in or register to add a comment.