Question

I just need help explaining it. solve the system of equation

Answer 1

Write out the equation

`\begin{gathered} y=(1)/(3)x-3 \\ 5x-3y=-3 \end{gathered}`

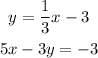
To solve this system of equation, the aprropriate method will be substitution

Substitute the expression for y into the second equation for y, we have

`5x-3((1)/(3)x-3)=-3`

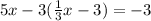
Expand the paranthesis we have

`\begin{gathered} 5x-x+9=-3 \\ \text{Simplify},\text{ by subtracting 9 from both sides } \\ 4x+9-9=-3-9 \\ 4x=-12 \end{gathered}`

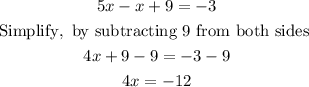
Divide both sides by 4, we have

`\begin{gathered} (4x)/(4)=-(12)/(4) \\ \text{Then} \\ x=-3 \end{gathered}`

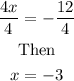
Since the value of x has been obtained, we substitute into the first equation

`\begin{gathered} y=(1)/(3)x-3 \\ \text{ recall x=}-3 \\ y=(1)/(3)(-3)-3 \\ y=-1-4 \\ \text{Hence } \\ y=-4 \end{gathered}`

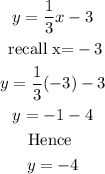
Therefore

x = -3, y= -4