Question

(a) List the intervals where f is increasing:(b) List the intervals where f is decreasing:(c) List the distinct y-values of the local maximums, if any exist:(d) List the distinct y-values of the local minimums, if any exist:(e) Find the y-value of the maximum, if it exists:(f) Find the y-value of the minimum, if it exists:

Answer 1

We are given the graph of a function and we are asked to determine the following:

part A) The intervals where "f" is increasing. A function increases when the values of "y" increase as the values of "x" increase. From the graph we notice that the function increases between x = -6 and x = -3, also between x = 3 and x = 6. This can be written in interval notation as:

`\lbrack-6,-3)\cup(3,6\rbrack`

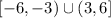
Part B. The function decreases when the values of "y" decrease as the values of "x" increase. We notice from the graph that the graph decreases between x = -3 and x = 3. Therefore, the intervals are:

`(-3,3)`

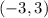
Part c and Part d. In the given domain of the function, there are only two extreme points, therefore, there are no local maxima or minima.

part e. The maximum value is the point "y" that is greater than other "y" points in the function in the given domain. Therefore, the maximum value is:

Therefore, the maximum value of "y" is 6.

Part f. The minimum value of "y" is the value that is the smallest of the function in the given domain. Therefore, from the graph we determine the following minimum point:

Therefore, the minimum value of "y" is -6.