Question

Ben wants to draw rectangles that each have an area of 30 square inches. The length and width of each rectangle are whole numbers of inches. Part A Decide if each statement about the possible rectangles Ben could draw is true or false Choose True or False for each statement. The rectangle can have a length of 10 inches and a width of 3 inches. O True O False The rectangle can have a length of 7 inches. O True O False The rectangle can have a width of 2 inches. O True O False The rectangle can have a length of 12 inches, a width of 3 inches, and a perimeter equal to its area. O True O False The rectangle can have a width of 5 inches and a perimeter that is less than 30 inches. O True O False

Answer 1

The area of a rectangle can be determined by the following equation:

`\text{Area = Lenght }*\text{ Width}`

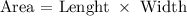
First statement: The rectangle can have a length of 10 inches and a width of 3 inches (True!).

`\text{Area = 10}*3\text{ = 30 square inches}`

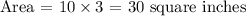
Second statement: The rectangle can have a length of 7 inches (False!). If the Area must be 30 square inches and the length and width of each rectangle are whole numbers of inches:

`30\text{ = 7}*\text{Width}`
`\text{Width = 4.28}`

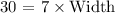
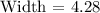
Width is not a whole number.

Thrid statement: The rectangle can have a width of 2 inches (True!)

`30\text{ = 2}*\text{Length}`
`\text{Length = 15}`

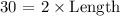
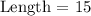
Fourth statement: The rectangle can have a length of 12 inches, a width of 3 inches, and a perimeter equal to its area (False!)

`\text{Area = 12}*3\text{ = 36 }\\e30`

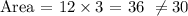
Fifth statement: The rectangle can have a width of 5 inches and a perimeter that is less than 30 inches (True!). Suppose that the length is 6 inches. The perimeter would be 5+5+6+6 = 22 inches and the area:

`\text{Area = 5}*6\text{ = 30 square inches}`

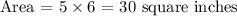
Therefore, the answers will be True-False-True-False-True.