Concept
Write two equations from the two-word problems.
a) The sum of 3 times x and 5 times y is 57
Sum means addition (+)
3 times x = 3x
5 times y = 5y
Therefore, their sum:
3x + 5y = 57 --------------------------- (1)
b) y is 1 more than twice the value of x.
'More than'Kindly means addition.
twice of x = 2x
y is 1 more than twice of x is y = 2x + 1
y = 2x + 1 ------------------------------------------- (2)
Next, solve equations 1 and 2 simultaneously to find x and y using the substitution method.
Substitute y in equation 2 into equation 1.
3x + 5y = 57
3x + 5(2x + 1) = 57
3x + 10x + 5 = 57
Collect like terms
3x + 10x = 57 - 5
13x = 52
Divide 13 on both side to get:
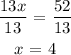
Next, substitute x in y = 2x + 1 to find the value of y.
y = 2(4) + 1
y = 8 + 1
y = 9
=
Final answer
The value of x + y is 4 + 9 = 13
x + y = 13