Question

A 45 gram sample of a substance that's used to sterilize surgical instruments has a k-value of 0.1474. N = Noe^ -kt No = initial mass (at time t = 0) N = mass at tim t k = a positive constant that depends on the substance itself and on the units used to measure time t = time, in daysFind the substance's half-life, in days. Round your answer to the nearest tenth.

Answer 1

4.7 days

1) Gathering the data

45gram

K = 0.1474

2) To find out the substance half-life, we have to plug into that formula the following data for the amount of mass

`\begin{gathered} N_0=45\text{ g} \\ N=(45)/(2)=22.5 \end{gathered}`

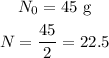
Since the half-life is the time a substance gets to half of its initial amount. So we can write out, remembering that e= 2.718:

`\begin{gathered} N=N_0\cdot e^(-kt) \\ 22.5=45\cdot2.718^(-0.1474t) \\ (22.5)/(45)=(45\cdot2.718^(-0.1474t))/(45) \\ (1)/(2)=2.718^(-0.1474t) \end{gathered}`

Now we can apply the logarithms to both sides:

`\begin{gathered} \log _e(1)/(2)=\log _ee^(-0.1474t) \\ -0.693=-0.1474t \\ t=4.71 \end{gathered}`

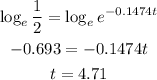
Hence, the answer is the half life is 4.7 days (rounded off to the nearest tenth)