Question

The parks department rents canoes at docks near each entrance.

Answer 1

`c\approx63\Rightarrow\text{ Option two}`

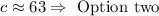
Step-by-step explanation: The doc=to door distance can be calculated using the Pythagorean theorem, which states the following:

`a^2+b^2=c^2\Rightarrow(1)`

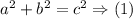
According to the diagram, the known and the unknowns for equation (1) are as follows:

`\begin{gathered} a=110m \\ b=90m \end{gathered}`

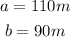
Plugging these values in equation (1) gives the following answer:

`(110)^2+(90)^2=c^2`

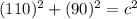
Solving for the c gives the answer, the steps are shown as follows:

`\begin{gathered} c^2=(110)^2+(90)^2 \\ c=√((110)^2+(90)^2) \\ c=√(12100-8100) \\ c=√(4000)=63.245 \\ c\approx63 \end{gathered}`

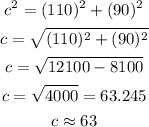
In conclusion, the answer is Option Second.