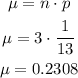Question

suppose you have an experiment where you draw three cards with replacement from a standard deck of 52 cards you didn't count the number of access drawn use this experience address each of the following question round solution to 4 decimal place

Answer 1

a) the random variable is:

x = the number of aces observed when you draw three random cards.

b) This experiment follows the binomial distribution because when you draw a card with replacement there are two options: it is an ace, or it is not an ace.

The binomial distribution has the next formula:

`P(x)=_nC_x\cdot p^x\cdot q^(n-x)^{}`

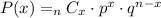
where:

P(x) = binomial probability

x = number of times for a specific outcome within n trials

nCx = number of combinations

p = probability of success on a single trial

q = probability of failure on a single trial

n = number of trials

In this case, the possible values of x are 0, 1, 2, and 3. The number of trials, n, is 3. The probability of success, p, that is, the probability of drawing an ace from a 52 cards deck is:

`p=(4)/(52)=(1)/(13)`

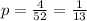
The probability of failure, q, that is not drawing an ace is:

`q=(48)/(52)=(12)/(13)`

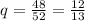
Therefore, the probability of drawing zero aces, that is, x = 0, is:

`\begin{gathered} P(0)=_3C_0\cdot((1)/(13))^0\cdot((12)/(13))^(3-0) \\ P(0)=1\cdot1\cdot(1728)/(2197) \\ P(0)=0.7865 \end{gathered}`

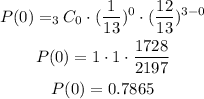
Therefore, the probability of drawing one ace, that is, x = 1, is:

`\begin{gathered} P(1)=_3C_1\cdot((1)/(13))^1\cdot((12)/(13))^(3-1) \\ P(1)=3\cdot(1)/(13)^{}\cdot((12)/(13))^2 \\ P(1)=0.1966 \end{gathered}`

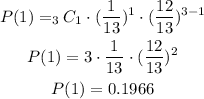
Therefore, the probability of drawing two aces, that is, x = 2, is:

`\begin{gathered} P(2)=_3C_2\cdot((1)/(13))^2\cdot((12)/(13))^(3-2) \\ P(2)=3\cdot((1)/(13))^2\cdot(12)/(13)^{} \\ P(2)=0.0164 \end{gathered}`

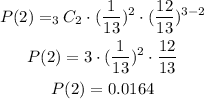
Therefore, the probability of drawing three aces, that is, x = 3, is:

`\begin{gathered} P(3)=_3C_3\cdot((1)/(13))^3\cdot((12)/(13))^(3-3) \\ P(3)=1\cdot((1)/(13))^3\cdot1 \\ P(3)=0.0004 \end{gathered}`

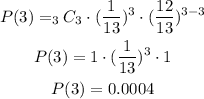
And the table is:

x | P(x)

0 | 0.7865

1 | 0.1966

2 | 0.0164

3 | 0.0004

c) The probability distribution of x is right-skewed (the probability is greater for the smaller values of x)

d) The mean in binomial distribution is calculated as follows:

`\begin{gathered} \mu=n\cdot p \\ \mu=3\cdot(1)/(13) \\ \mu=0.2308 \end{gathered}`