Given:
The area of the pond, A=63 m^2.
Let l be the length and w be the width of the rectangular pond.
It is given that the pond has length 2m more than twice it's width.
Hence, the expression for the length of the pond is,
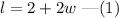
Now, the area of the rectangular pond can be expressed as,
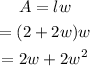
Since A=63, we get
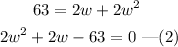
The above equation is in the form of a quadratic equation given by,
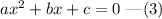
Comparing equations (2) and (3), we get a=2, b=2, c=-63 and x=w.
Solve equation (2) for w using discriminant method.
![\begin{gathered} w=\frac{-b\pm\sqrt[\square]{b^2-4ac}}{2a} \\ =\frac{-2\pm\sqrt[]{2^2-4*2*(-63)}}{2*2} \\ =\frac{-2\pm2\sqrt[]{127}}{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hzotrxpqvp227otea9al7z5oovkudfjcgl.png)
Since width w cannot be negative ,
![\begin{gathered} w=\frac{-2+2\sqrt[]{127}}{4} \\ =5.13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hc8lftr2hcrk6t1rz8y5yup9g94a6xu4b5.png)
Put w=5.13 in equation (1).
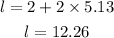
Therefore, the length of pond is approximately 12.26 m and its width is approximately 5.13 m.