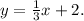Recall that the slopes of two perpendicular lines, satisfy that:

Therefore, the slope of the line perpendicular to -3x-2 must-have slope
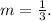
Now, to determine the equation of the line, we will use the following formula for the equation of a line with slope m, that passes through the point (x₁,y₁):
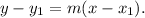
Substituting (x₁,y₁)=(-7,-1/3), and m=1/3 in the above formula, we get:
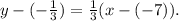
Simplifying the above result, we get:
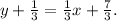
Recall that the slope-intercept form of the equation of a line is:
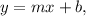
where b is the y-intercept and m is the slope.
Taking the equation of the line to its slope-intercept form we get:
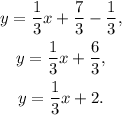
Answer: