25
Step-by-step explanation
to solve this we need to apply the secant-tan rule, it says
if a secant and tangent are drawn to a circle form the same external point, the product of the lengths of the secant and its external segement equals the square of the length of the tangent segment
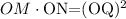
so,
Step 1
indentify
OM= DE (unknown value)=DC+CE=DC+9
ON=CE=9
OQ=AE=15
replace

so, we get that
DC=16
Step 2
Also, we know
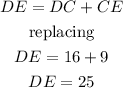
therefore, the answer is
25
I hope this helps you