Question

I need help on this question

Answer 1

We need to complete the square of the next two equations:

`\begin{gathered} x^2-4x \\ \text{and} \\ y^2-6y \end{gathered}`

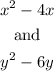
We know that:

`(x-2)^2=x^2+2\cdot x\cdot(-2)+(-2)^2=x^2-4x+4`

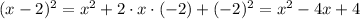
and:

`(y-3)^2=y^2+2\cdot y\cdot(-3)+(-3)^2=y^2-6y+9`

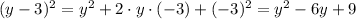
Adding and subtracting 4 and 9 to the original equation, we get:

`\begin{gathered} x^2+y^2-4x-6y+8=0 \\ x^2+y^2-4x-6y+8+4-4+9-9=0 \\ (x^2-4x+4)+(y^2-6y+9)+(8-4-9)=0 \\ (x-2)^2+(y-3)^2-5=0 \\ (x-2)^2+(y-3)^2=5 \end{gathered}`

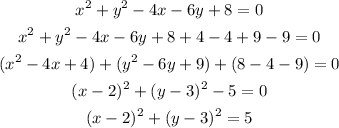
This equation has the next form:

`(x-h)^2+(y-k)^2=r^2`

which corresponds to a circle centered at (h,k) with radius r. Then, in our equation, the center is (2,3) and the radius is √5.