Question

Question 2 (2 points)Determine the following of the function y = 0.7log3(x).• DomainRange• X-intercept• Y-interceptAsymptote..

Answer 1

Recall that

`\log _ax`

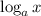
is defined for all positive real numbers, therefore:

`\text{Dom}(0.7\log _3(x))=(0,\infty)\text{.}`

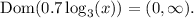
Also, since the range of log_3(x) is all real numbers, then:

`Ran(0.7\log _3(x))=(-\infty,\infty).`

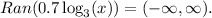
Now, to find the x-intercept, we set y(x)=0:

`0.7\log _3(x)=0.`

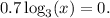
Dividing the above equation by 0.7 we get:

`\begin{gathered} (0.7)/(0.7)\log _3(x)=(0)/(0.7), \\ \log _3(x)=0. \end{gathered}`

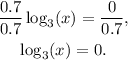
Solving the above equation for x we get:

`\begin{gathered} 3^(\log _3(x))=3^0, \\ x=1. \end{gathered}`

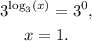
Therefore, the x-intercept has coordinates (1,0).

Since the function is only defined at (0,∞), there is no y-intercept.

Finally, the function has an asymptote at x=0.

Answer:

Domain:

`(0,\infty).`

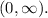
Range:

`(-\infty,\infty).`

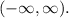
X-intercept:

`(1,0)\text{.}`

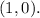
Y-intercept: There is no y-intercept.

Asymptote:

`x=0.`