Answer
- Question 1:
The equation for the number of memberships is:
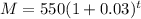
- Question 2:
The number of memberships in 2020 will be 964
Step-by-step explanation
Problem Statement
We are told that a gym sold 550 memberships in 2001 and that the number of memberships sold has increased by 3% every year since then.
We are asked to find:
1. The equation for the number of memberships sold for t years after 2001.
2. The number of memberships sold by 2020.
Solution
Question 1:
- The question tells us that the number of memberships sold in 2001 is 550. This is the initial value of our equation.
- We are told that the number of memberships increases 3% every year since 2001.
- This implies that:
![\begin{gathered} In\text{ year 2001, the number of memberships sold }=550 \\ \\ In\text{ year 2002, 1 year from 2001, the number of memberships sold}=Amount\text{ sold in 2001 + 3\% of the Amount sold in 2001} \\ T\text{he number of memberships sold in 2002}=550+(3\text{ \% }*550)=550+550(0.03)=550(1+0.03) \\ \\ In\text{ year 2003, 2 years from 2001, the number memberships sold}=\text{Amount sold in 2002 + 3\% of the Amount sold in 2002} \\ The\text{ number of memberships sold in 2003}=(550+(3\text{ \% }*550))+(3\text{ \%}*(550+(3\text{ \% }*550)) \\ =550\mleft(1+0.03\mright)+0.03\mleft(550\mleft(1+0.03\mright)\mright) \\ \text{ We can factorize this expression as follows:} \\ =550\mleft(1+0.03\mright)(1+0.03) \\ =550(1+0.03)^2 \\ \\ In\text{ year 2004},\text{ 3 years from 2001, the number of memberships sold}=Amount\text{ sold in 2003 + 3\% of the Amount sold in 2003} \\ =550(1+0.03)^2+3\text{ \% (}550(1+0.03)^2) \\ =550(1+0.03)^2+0.03(550(1+0.03)^2) \\ \text{ We can factorize again:} \\ 550(1+0.03)^2(1+0.03) \\ =550(1+0.03)^3 \end{gathered}]()
- Observing the above illustration, we can see a pattern. This pattern is that:
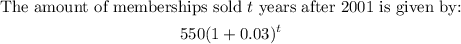
- Thus, we have the equation for the number of memberships sold t years after 2001 to be:
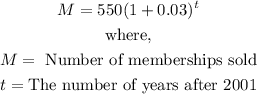
Question 2:
- We are asked to calculate the number of memberships the gym would sell by 2020.
- First, we need to find the value of t since it is the only variable in our formula. We have already defined t to be the number of years after 2001.
- Thus, t can be gotten as follows:
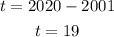
- Now that we have t, we can find the number of memberships as follows:
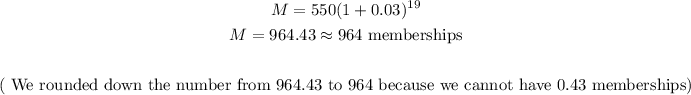
- Thus, the number of memberships in 2020 will be 964
Final Answer
- Question 1:
The equation for the number of memberships is:
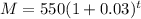
- Question 2:
The number of memberships in 2020 will be 964