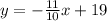Question

Find the equation of the line passing through the points (10,8) and (-10,30). Write your answer in the form

Answer 1

The equation of a line in slope-intercept form is given by:

`y=mx+b`

Where m is the slope and b is the y-intercept.

We know two points on the line: (10,8) and (-10,30).

The slope can be found by using the following formula:

`m=(y2-y1)/(x2-x1)`

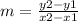
Where (x1,y1) and (x2,y2) are the coordinates of two points on the line. By replacing the known coordinates we obtain:

`m=(30-8)/(-10-10)=(22)/(-20)=-(11)/(10)`

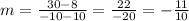
The y-intercept can be found by replacing the slope and one of the points in the slope-intercept formula, and solving for b:

`\begin{gathered} 8=-(11)/(10)\cdot10+b \\ 8=-11+b \\ 8+11=b \\ b=19 \end{gathered}`

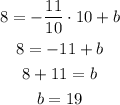
Thus, the equation of the line is:

`y=-(11)/(10)x+19`