Question

Two charges, q1 -2.00 X 10-6 C and q2 = -1.80 X 10-5 C, are separated by a distance, L, of 4.00 m. A third charge, q3 = 1.50 X 10-6 C, is placed somewhere between q1 and q2, where the net force exerted on q3 by the other two charges is zero. Determine the location of q3.

Answer 1

Given:

The charges are

`\begin{gathered} q1=-\text{ 2}*10^(-6)\text{ C} \\ q2=-1.8*10^(-5)\text{ C} \\ q3=1.5*10^(-6)\text{ C} \end{gathered}`

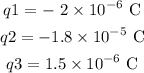
The distance between q1 and q2 is L = 4 m.

To find the location of q3 where forces due to q1,q2 on q3 are zero.

Step-by-step explanation:

Let the distance between q1 and q3 be x m, then the distance between q2 and q3 be (4-x) m.

The force on q3 due to q1 will be equal to the force on q3 due to q2.

`\begin{gathered} (kq1q3)/(x^2)=(kq2q3)/((4-x)^2) \\ q1(4-x)^2=q2(x)^2 \\ q1(16+x^2-8x)=q2x^2 \\ (q1-q2)x^2-8xq1+16q1=0 \end{gathered}`

On substituting the value, x will be

`\begin{gathered} (2*10^(-6)-1.8*10^(-5))x^2-8*(2*10^(-6))x+16*2*10^(-6)\text{ =0} \\ -16*10^(-6)x^2-16*10^(-6)x+32^*10^(-6)=0 \\ -16(x^2+x-2)=0 \\ x^2+2x-x-2=0 \\ x(x+2)-1(x+2)=0 \\ x=1,-2 \end{gathered}`

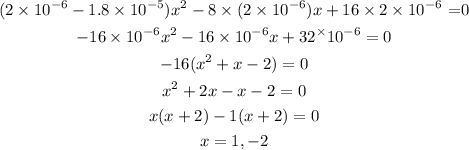
The value of x cannot be negative, so x=1.

The distance between q1 and q3 is 1 m and the distance between q2 and q3 is (4-1)=3 m