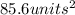Question

Find the area of the following regular polygons. Round all answers to nearest 10th

Answer 1

Step 1

Draw the regular polygon to find out how many triangles are in it.

We can, therefore, conclude the regular polygon has 5 triangles in it

Step 2

Find the area of 1 triangle

`\begin{gathered} \text{The angle at the center = 360}^o \\ \text{But since they are 5 triangles, each will have an angle of }(360)/(5)=72^o \end{gathered}`

Since the two sides of each triangle are radius, then they share the same angle. Hence,

`\begin{gathered} \text{The angle at the base of each triangle is given by} \\ 180=72+x+x \\ 180-72=2x \\ (2x)/(2)=(108)/(2) \\ x=54^o \end{gathered}`

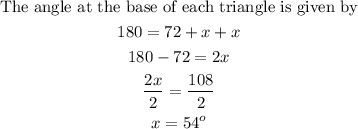
We can then find the k and y thus

`\begin{gathered} \sin 54=(k)/(6) \\ k=\text{ 6sin54} \\ k=\text{ 4.854101966 units} \\ \cos 54=(y)/(6) \\ y=6\cos 54 \\ y=3.526711514\text{ units} \\ 2y=7.053423028 \end{gathered}`

The area of one of the triangles is

`\begin{gathered} A=(1)/(2)* base(2y)* height(k) \\ A=(1)/(2)*7.053423028*\text{4.854101966} \\ A=17.11901729\text{ units} \end{gathered}`

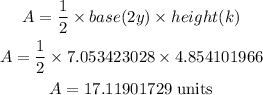
The area of the 5 triangles will be

`17.11901729\text{ }*5=85.59508647unit^2`

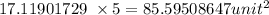
Hence the area of a regular polygon to the nearest tenth is given as;

`85.6units^2`