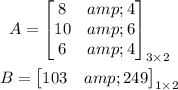
1) Notice that there are three students: Sean, Kevin, and Bill and there are 2 schools JJC and CSU. In addition to this, there's the cost per credit. So we can write out the following Matrix A, for the credits:

Note that Matrix A, in this case, works as a table. On the Matrix on the left, we have the name of the students, and at Matrix A, we have each row the credits each student is taking.
2) So now:
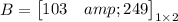
Notice that we multiply A by B we'll get the cost for every student.
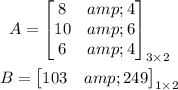
And that is the answer.