Question

I need help with this problem for my discussion post

Answer 1

Given: An absolute inequality

`\lvert{2x+3}\rvert=15`

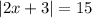
Required: To solve the given absolute inequality.

Step-by-step explanation: The absolute rule states

`\begin{gathered} If\text{ }\lvert{x}\rvert=a,\text{ }a>0\text{ ,then} \\ x=a\text{ or }x=-a \end{gathered}`

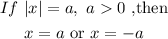
Hence for the given problem, we have

`2x+3=15\text{ or }2x+3=-15`

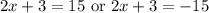
Solving these two equations

`\begin{gathered} 2x=12\text{ or }2x=-18 \\ \end{gathered}`

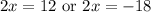
Which gives the value of x as

`x=6\text{ or }x=-9`

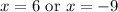
Hence the equation given can have two solutions.

Final Answer: The given equation can have two solutions as x=6 or x=-9.