To answer this question we will set and solve a system of equations.
Let A be the time (in hours) that it would take Company A to clear the parcel of land alone, and B be the time (in hours) that it would take Company B to clear the parcel of land alone.
Since working together, the two companies can clear the parcel of land in 8 hours, and wirking alone, it would take Company A 10 hours longer than Company B, then we can set the following system of equations:
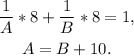
Substituting the second equation in the first one we get:

Simplifying the above result we get:
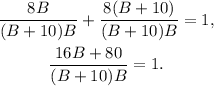
Multiplying the above result by (B+10)B we get:
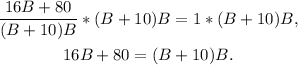
Simplifying the above result we get:
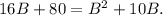
Subtracting 16B+80 from the above result we get:

Using the quadratic formula we get:

Since a negative value of B has no real meaning, we get that:
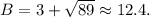
Answer: 12.4 hours.