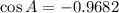To find the value f rthe cosine function we will us the identity:
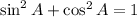
We know that the sine of A i 1/4 then we have:
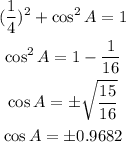
Now, we need to determine which sign to choose. Since the sinA lies in th second quadrant thismeans that tehe coosine als lies in the quadrant; furthermore, we know that the cosine is negative in the second and thirsd quadrants whichmeans that we need to use the negative sign. Therefoore: