Given the following exponential equation:
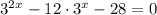
Note: the given equation is a quadratic equation
Let u = 3ˣ
So, the equation will be:

so,
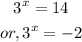
The negative result will be rejected because the range of the exponential function is greater than zero
So, the exact value of x will be as follows:
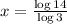
The approximate solution using the calculator will be:
x = 2.40