Question

A marine biologist is preparing a deep-sea submersible for a dive. The sub stores breathing air under high pressure in aspherical air tank that measures 63.0 cm wide.The biologist estimates she will need 5300. L of air for the dive. Calculate the pressure to which this volume of air must becompressed in order to fit into the air tank. Write your answer in atmospheres. Round your answer to 3 significant digits.X5 ?EdoloAr184

Answer 1

The following assumptions are made:

1. Air behaves like an ideal gas throughout the process.

2. The initial pressure will be equal to the atmospheric pressure at sea level, 1atm.

3. The temperature remains constant.

Taking into account the above, we can apply the Boyle-Marriote Law that relates the change in pressure and volume at constant temperature. The equation tells us:

`P_1V_1=P_2V_2`

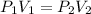
Where,

P1 is the initial pressure, 1atm

V1 is the initial volume, 5300L

P2 is the final pressure inside the air tank, this is our unknown

V2 is the final volume, this will be calculated using the volume equation for a sphere:

`V_2=(4)/(3)\pi r^3`

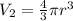
r is the radius of the sphere, 63.0cm/2=31.5cm

So, the volume of the air tank will be:

`\begin{gathered} V_2=(4)/(3)\pi*(31.5cm)^3=13.1*10^4cm^3 \\ V_2=13.1*10^4cm^3*(1L)/(1000cm^3)=131L \end{gathered}`

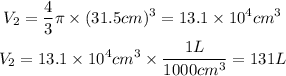
We clear P2 and replace the known data:

`\begin{gathered} P_2=(V_1P_1)/(V_2) \\ P_2=(5300L*1atm)/(131L)=40.5atm \end{gathered}`

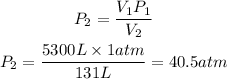
The air must be compressed at 40.5atm

Answer: 40.5