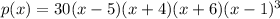Question

4. Create an equation for a 6th degree polynomial that only has the zeros of x=5, -4, -6, 1 with a y-intercept of 3600. Explain how you found your equation.

Answer 1

Since the y-intercept of the polynomial must be 3600, then:

`p(0)=3600`

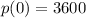
Since the only zeroes of the polynomial must be x=5, -4, -6 and 1, then the factors of the polynomial, are:

`\begin{gathered} (x-5) \\ (x+4) \\ (x+6) \\ (x-1) \end{gathered}`

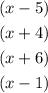
Let the multiplicity of the factor (x-1) be equal to 3 and let the multiplicity of the rest of the factors to be equal to 1. Then:

`p(x)=a(x-5)(x+4)(x+6)(x-1)^3`

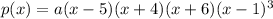
Where a is a constant. Notice that the degree of that polynomial is 6. Evaluate it at x=0 to find the value of a that makes the y-intercept to be equal to 3600:

`\begin{gathered} p(0)=a(0-5)(0+4)(0+6)(0-1) \\ =a(-5)(4)(6)(-1) \\ =120a \end{gathered}`

Since p(0)=3600, then:

`\begin{gathered} 3600=120a \\ \Rightarrow a=(3600)/(120) \\ \Rightarrow a=30 \end{gathered}`

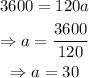
Therefore, the following polynomial is a 6th degree polynomial with zeroes at the values of 5, -4, -6 and -1 with a y-intercept equal to 3600:

`p(x)=30(x-5)(x+4)(x+6)(x-1)^3`