Step-by-step explanation
To solve the question, we will first apply a similar triangle theorem
Similar triangles are triangles that have the same shape, but their sizes may vary.
so, we can compare similar sides to get x before we get the perimeter
Thus
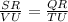
Hence
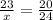
Solving for x
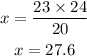
Thus, we will have
Then the perimeter will be:
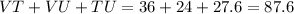
Therefore, the perimeter of the triangle TUV is 87.6