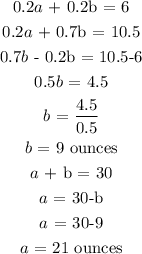Answer:
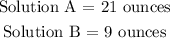
Step-by-step explanation:
Let the number of ounces of solution A be a
Let the number of ounces of solution B be b
The sum total of the ounces is 30
Thus:
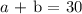
Now, let us work with the percentages
Mathematically, we have it that:

The two linear equations we are to solve simultaneously are:
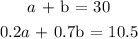
Multiply equation 1 by 0.2 and equation 2 by 1: we have: