Question

PLEASE HELP ME QUICKLY!This is what I got so far... I don’t need a long explanation. I just need to know what to put next to get the answer. y - k = 1/4p (x-h)^290 - 10 = 1/4p (300 - 0)^280 = 1/4p 300^2p = ? please finish the rest of the problem.

Answer 1

Ok, so

We know that the equation for a parabola is given by:

`y-k=(1)/(4p)(x-h)^2`

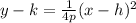
The problem tells us that the lowest height of the cable is 10 feet above the ground, and the pillars rise 90 feet above the road. Also, the pillars are 600 feet apart and the lowest height is reached halfway between them. So, this is located in the center of the total distance. (300m).

Then, the vertex (h,k) for this parabola will be:

`(300,10)`

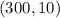
If we replace:

`y-10=(1)/(4p)(x-300)^2`

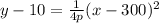
Now, we could assign some values of the cable for "x" and "y". These values would be:

`\begin{gathered} y=90 \\ x=600 \end{gathered}`

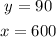
Replacing and solving the equation for p:

`\begin{gathered} 90-10=(1)/(4p)(600-300)^2 \\ 80=(1)/(4p)(300)^2 \\ 80=(1)/(4p)(90000) \\ 4p=(90000)/(80) \\ 4p=1125 \\ p=281.25 \end{gathered}`

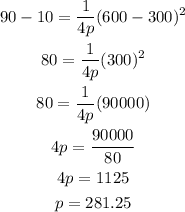
The equation for this parabola will be:

`y-10=(1)/(1125)(x-300)^2`

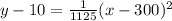
We want to find "y" such that x=450ft. For this, replace:

`\begin{gathered} y-10=(1)/(1125)(450-300)^2 \\ y-10=(1)/(1125)(22500) \\ y-10=20 \\ y=20+10 \\ y=30ft \end{gathered}`

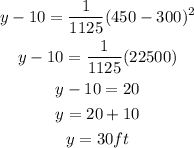
Therefore, the height of the cable from the road at a point 150 feet horizontally from the center of the bridge is 30ft.

Notice that the parabola on a coordinate plane is