Question

Choose the trigonometric expression below that is equal to sinxcotxsecx/cosxcscx to form a trigonometric identity. cosxcscx secxsinx cosxtanx

Answer 1

The given expression is:

`(\sin x\cot x\sec x)/(\cos x\csc x)`

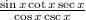
By using trigonometric identities we have that:

`(\sin x)/(\cos x)=\tan x`

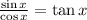
Then, replace sinx/cosx in the expression by tanx:

`(\sin x\cot x\sec x)/(\cos x\csc x)=(\tan x\cot x\sec x)/(\csc x)`

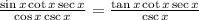
Now:

`\tan x=(1)/(\cot x)`

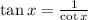
Thus:

`\tan x\cdot\cot x=(1)/(\cot x)\cdot\cot x=(\cot x)/(\cot x)=1`

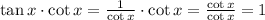
Replace tanx*cotx in the expression by 1:

`(\tan x\cot x\sec x)/(\csc x)=(1\cdot\sec x)/(\csc x)=(\sec x)/(\csc x)`

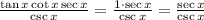
Finally:

`\begin{gathered} \sin x=(1)/(\csc x) \\ \text{and} \\ (1)/(\cos x)=\sec x \\ \text{Thus} \\ (\sec x)/(\csc x)=(\sin x)/(\cos x) \end{gathered}`

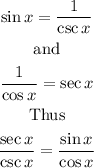
And as we said in the first trigonometric identity sinx/cosx=tanx, thus:

`(\sin x)/(\cos x)=\tan x`

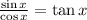
Answer: the trigonometric expression that is equal to the given is tanx