Question

Find the average rate of change of the following line WITHOUT CALCULATING. y=18 on [1000,10000]

Answer 1

The average rate of change of the function y = 18 on the interval [1000, 10,000] is ZERO

SOLUTION

Problem Statement

The question wants us to find the average rate of change of the function y = 18 on the interval [1000, 10,000].

Method

- The function given is a constant function. This means that for every value of x from -∞ to +∞, the value of the function will always be y = 18.

- Since y is a function of x (albeit a constant function of x), it can be written as y = f(x).

- With these in mind, we can find the average rate of change of the function using the formula given below:

`\begin{gathered} \bar{\Delta}=(f(b)-f(a))/(b-a) \\ \text{where} \\ \lbrack a,b\rbrack\text{ is the interval for which we want to know the rate of change of the function }f(x) \end{gathered}`

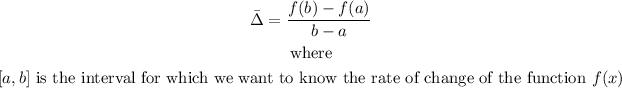
- Note that since the function is a constant function, we should expect that its rate of change should be ZERO since the function is constant throughout despite the value of x.

Let us apply the formula above to find the average rate of change of the given function.

Implementation

The average rate of change of the function y = 18 is gotten below:

`\begin{gathered} b=10,000,a=1000 \\ f(b)=f(10,000)=18\text{ (Since the function does not change)} \\ f(a)=f(1000)=18\text{ (Since the function is constant)} \\ \\ \therefore\bar{\Delta}=(18-18)/(10,000-1000)=(0)/(9,000) \\ \\ \therefore\bar{\Delta}=0 \end{gathered}`

Final Answer

The average rate of change of the function y = 18 on the interval [1000, 10,000] is ZERO