Question

Miguel found a coin in the cushions of his car and thought to himself, “What are the chances that, if I flip this coin twice, the same side will come face up both times?” Answer the following questions regarding this:Use a tree diagram to show the different possible outcomes if Miguel were to flip his coin twice.What is the probability that Miguel will get the same side of the coin to land face up if he flips it twice? How is that different from the probability that he will get two heads? Miguel calculated the probability and then decided to try it out. He did two flips 25 times and didn’t get the exact number of same side outcomes as his calculated probability predicted. Does that mean that he did his calculations incorrectly? How do you know? Fully explain your answer

Answer 1

We are given that a person tosses a coin twice. A tree of possible outcomes is the following:

Where "H" is head and "T" is tails.

The possible outcomes are then:

`\begin{gathered} HH \\ HT \\ TH \\ TT \end{gathered}`

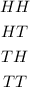
There are 4 possible outcomes.

Part 2. To determine the probability of getting two tails we notice that from the 4 possible outcomes 1 is TT, therefore, the probability is:

`P(TT)=(1)/(4)`

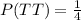
The probability of getting two heads is determined also using the fact that from the 4 possible outcomes only one is HH, therefore:

`P(TT)=(1)/(4)`

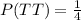
This means that the probabilities are the same.

The reason why he didn't get the exact number of times as predicted might be due to the fact there might be other variables affecting the outcome. Or that can be due to the fact that the number of tosses is not enough to see a tendency.