ANSWER:
a. 3, 9, 27, 81, 243
b. 3
c. 3^n
d. 88572
Explanation:
a.
A geometric sequence has the following form:
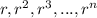
We calculate the first 5 numbers like this:
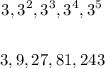
b.
The common ratio is calculated like this:
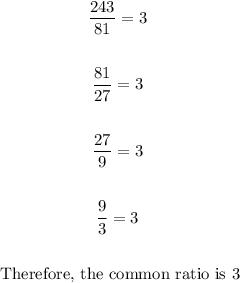
c.
We have that the equation of the sequence is the following:
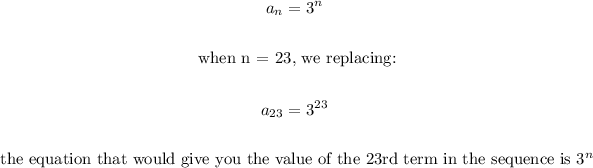
d.
The sum of the first 10 terms is given as follows:
