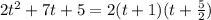Question

Factor trinomials using trial and error 2t^2 + 7t + 5

Answer 1

`2t^2+7t+5=2(t+1)(t+(5)/(2))`

Step-by-step explanation

To factor a trinomial, we want to write it in terms of the zeros (or roots) of the function,

`f(t)=(t-t_1)(t-t_2)`

Sometimes we can find one or both zeros using trial and error, by replacing t with values around 0 (-2, -1, 0, 1, 2, etc) and see if any of them make the function zero.

In this case, there is an independent term, so t = 0 is not a zero. Let's try with t = 1,

`f(1)=2\cdot1^2+7\cdot1+5=2+7+5=14`

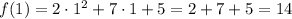
So t = 1 is not a zero.

Let's try with t = -1,

`f(-1)=2(-1)^2+7(-1)+5=2-7+5=0`

Hence, t = -1 is a zero. One of the factors is (t + 1).

Then, to find the other factor we can use this one, and divide the trinomial by the known factor. The result will be the unknown factor,

So we have that the other factor will be (2t + 5). Usually, to identify the zeros more quickly, we factor out the coefficients of the variable. Thus, if we factor 2 out,

`(2t+5)=2\mleft(t+(5)/(2)\mright)`

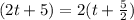
Hence, the factored form of the trinomial is,

`2t^2+7t+5=2(t+1)\mleft(t+(5)/(2)\mright)`