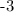Question

Sketch the graph, showing one complete cycle. State the period and amplitude, and the greatest and least values of yy=3sin(θ−π/2)

Answer 1

Step-by-step explanation:

Consider the following general periodic function:

`y=a\sin b(\theta\text{ -h})\text{ +k}`

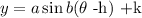
where

a= amplitude

b = frecuency

h= phase translation

k= vertical translation

2π/ |b| = period

Now, consider the following periodic function:

`y=3sin(\theta\text{ -}(\pi)/(2))`

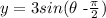
Applying the definition given at the beginning of this explanation, we can see that:

a = amplitude = 3

2π/ |b| = period = 2π/|1| = 2π

Then, the graph of the given function is:

Notice that the greatest and least values of y are 3 and -3 respectively.

We can conclude that the correct answer is:

Answer:

Graph:

Period:

`2π`

Amplitude:

`3`

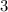
The greatest value of y (coordinate y of the maximum point):

`3`

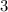
The least value of y (coordinate y of the minimum point):

`\text{ -3}`